Точная механика работы весла

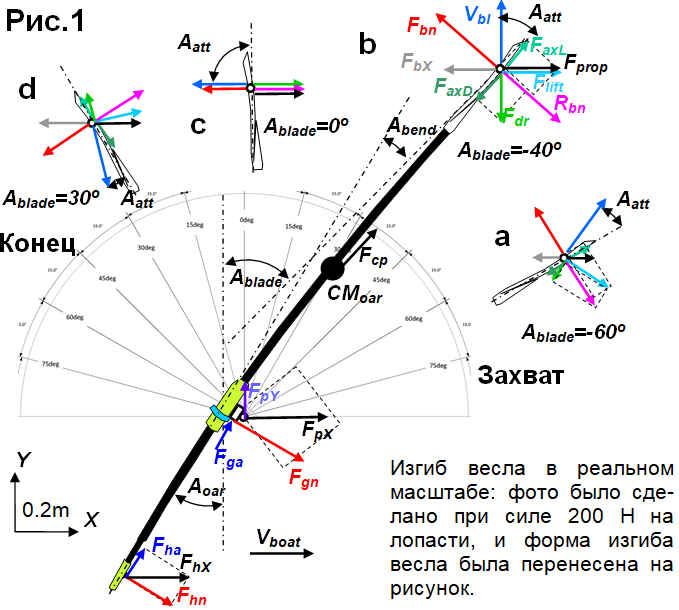
Мы продолжаем анализ механики весла с двумя целями: 1) проверить сумму сил на весле с измеренными силами на вертлюге-оси; 2) соотнести измеренные силы с продвижением системы гребец-лодка. Четыре момента и пять сил были измерены на каждом весле в последнем эксперименте, моменты были описаны в НБГ 2020/10-11, силы следующие: нормальная сила на вертлюге Fgn, аксиальная сила на вертлюге Fga, сила X (вперед) на оси FpX, сила Y (в сторону) на оси FpY (Рис.1) и сила Z (вертикальная) на оси FpZ (ортогональна плоскости и не показана на Рис.1). Два угла весла в горизонтальной Aoar и вертикальной плоскости Aov измерялись на внутреннем рычаге весла, что доводит общее количество изменяемых переменных до 11 на каждом весле.

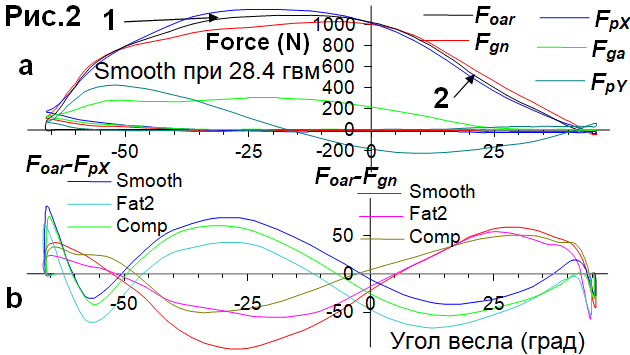
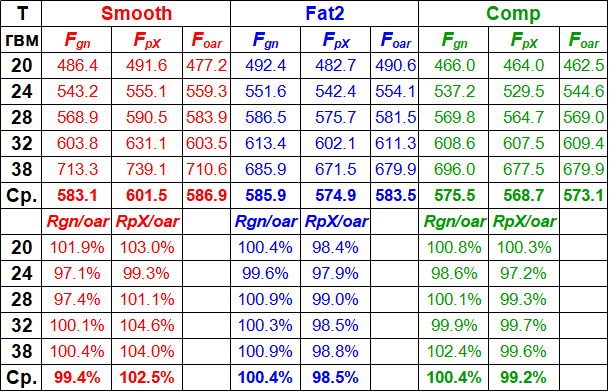
Нормальные силы на рукоятке Fhn и лопасти Fbn были рассчитаны по измеренным моментам и точкам приложения сил (НБГ 2020/10). Сначала, было проверено, равняется ли сумма сил на весле Foar=Fhn+Fbn измеренной нормальной силе на вертлюге Fgn. Также сравнивалась продвигающая сила на оси FpX (Рис.2). Средние величины за проводку (Табл.1) были близки с различиями в пределах ±1.5%, что свидетельствует о точности измерений: Fgn была несколько выше Foar, и FpX была несколько ниже. Кривые этих сил имели несколько различную форму: Foar была выше, чем Fgn и ниже FpX до перпендикуляра весла (1), но затем различия меняли знак (2), так что кривые разностей сил оказались почти зеркальными (Рис.2,b)

Это было удивительно, поскольку продвигающая сила на оси FpX зависит от угла весла, так что среднее значение FpX должно быть ниже, чем Fgn, если только осевая сила Fga не достаточно компенсирует влияние угла весла, и похоже, она это делает.

Следующим вопросом стала верификация продвигающей силы внутри системы гребец-лодка (НБГ 2019/01-02) в сравнении с продвигающей силой на лопасти. Изгиб оси весла, вызванный моментом на внешнем рычаге Mout создает дополнительный угол на лопасти Abend, который был определен экспериментально и был почти одинаков для всех весел (даже для extra-soft весла Fat2):

Abend = 0.02652 Mout                                                             (1)

Это означает, при пиковых усилиях, угол лопасти отличается почти на 10 град от угла весла, измеренного на внутреннем рычаге (Рис.1). Продвигающая сила на лопасти FbX рассчитывалась, как:

FbX = Fbn cos(Aoar + Abend)                                                 (2)

Продвигающая сила системы рассчитывалась, как разность между Х компонентами сил на оси и рукоятке:

Fsys = FpX - FhX = FpX – (Fhn cos(Aoar) + Fha sin(Aoar))     (3)

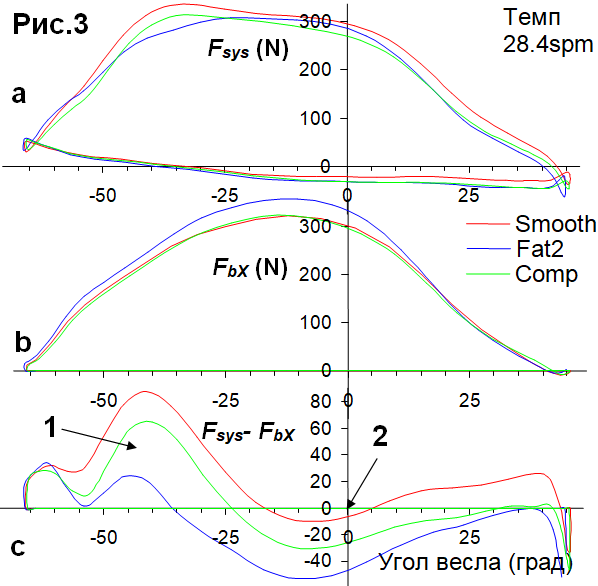
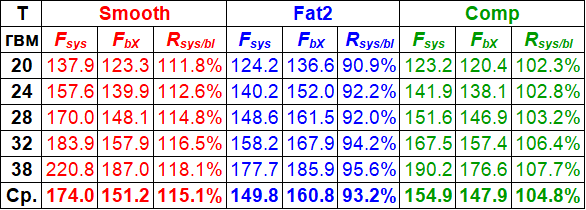
Было обнаружено, что сила Fsys была выше от захвата до угла весла примерно -25 град (Рис.3), затем сила FbX доминировала около перпендикуляра весла, и наконец, Fsys была снова выше до конца проводки. Эти различия между FbX и Fsys значительно отличались между типами лопастей (Рис.3,c) также, как и отношения их средних значений за проводку: у Smooth, средняя Fsys была на 15.1% выше, чем FbX, у Comp – на 4.8% выше, и у Fat2 – на 6.8% ниже (Табл. 2). Первое подозрение после этих парадоксальных открытий было то, что они объясняются ошибками в калибровке датчиков, но это выглядит невероятным, поскольку те же самые датчики на вертлюге и оси использовались с различными веслами с интервалом около получаса. Датчики моментов на весле также были откалиброваны одним и тем же датчиком силы и досконально проверены.

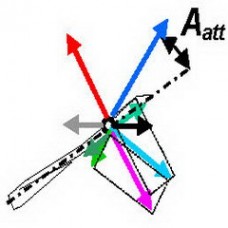
Гипотеза, объясняющая этот парадокс следующая. Когда лопасть двигается в воде с определенной скоростью Vbl и под углом атаки Aatt (между осью лопасти и вектором ее скорости в воде, Рис.1), это создает две силы: соосную со скоростью и противоположно направленную силу сопротивления Fdr и перпендикулярную силу гидро-лифта Flift. Векторная сумма этих двух сил в ортогональном к лопасти направлении – есть сила реакции на лопасти Rbn, которая имеет одинаковую величину и противоположное направления к силе действующей на лопасти Fbn, которая использовалась для расчета ее продвигающей силы. Однако, эти силы сопротивления Fdr и лифта Flift также проектируются и на ось лопасти и создают осевые (аксиальные) силы, которые действуют в противоположных направлениях. Величины этих осевых сил зависят от угла атаки Aatt, а также от коэффициентов лифта Cl и сопротивления Cd лопасти, а последние зависят от ее характеристик (формы, гладкости поверхности и т.п.). Результирующая осевых компонентов сил передается вдоль оси весла и влияет на измеряемые силы на оси и вертлюге, а значит – и на продвигающую силу системы гребец-лодка.

После захвата, при острых углах атаки (Рис.1,a-b), сила лифта Flift наиболее значительна, ее осевой компонент направлен вперед и преобладает над осевой силой сопротивления Fdr, направленной назад. Это может быть причиной тому, что продвигающая сила системы была выше, чем таковая на лопасти при углах весла от -50-25 перед перпендикуляром (Рис.3,1).

При углах весла близких к 0 град в середине проводки (Рис.1,с), вектор скорости лопасти почти перпендикулярен к ее оси (угол атаки около 90 град), сила лифта отсутствует и лишь сила сопротивления действует на лопасть, которая здесь не имеет осевого компонента. У лопастей Smooth, здесь был почти нулевой баланс продвигающих сил системы Fsys и лопасти FbX (Рис.3,2), что логично, но другие типы лопастей имели отрицательную разность Fsys-FbX: у Fat2 сила на лопасти была значительно выше (из-за ее большей площади и более короткого действующего внешнего рычага – легкой передачи), но без выигрыша в продвижении системы, а Comp проигрывали в продвижении системы (?) при аналогичных усилиях на лопасти со Smoothie. Мы можем лишь догадываться, что причиной этого может быть вращение лопасти в воде, которое создает некоторое сопротивление, потребляет энергию и снижает продвижение системы таким образом.

После «перпендикуляра» до конца проводки, угол атаки становится все острее, и осевые силы снова влияют на продвижение системы: осевой компонент силы лифта толкает весло вперед, а осевое сопротивление – тянет его назад. Лопасти Smooth выглядят здесь наиболее эффективными и имеют положительный баланс Fsys-FbX, что можно отнести к меньшей силе сопротивления без полосок Vortex.

Дополнительный фактор, влияющий на баланс сил – центробежная сила Fcp , которая возникает при вращении весла, поскольку центр его массы расположен вне оси вращения на внешнем рычаге, и эта сила всегда осевая. «До перпендикуляра», эта сила направлена вперед и увеличивает продвижение системы, после него – работает назад и снижает продвижение. Несмотря на то, что эта сила должна быть достаточно мала, она все же может влиять на баланс продвигающих сил системы и лопасти, который был выше «до перпендикуляра» и ниже – после него, что выглядит логичным.

В заключении, основываясь на открытых выше данных, весла Fat2 показали более высокую продвигающую силу на лопасти из-за их большей площади и укороченного внешнего рычага, но это преимущество не было конвертировано в продвижение системы гребец-лодка. Наоборот, более низкие продвигающие силы на лопастях Smooth и Comp могли быть компенсированы увеличением скорости лопасти в воде из-за удлинённого внешнего рычага, что создавало дополнительный гидро-лифт, переносимый через осевую силу в продвижение системы. Кроме того, Smooth и Comp могли иметь более низкое сопротивления по сравнению с Fat2 из-за их меньшей площади, что также позитивно влияло на продвижение системы.

Полный анализ продвигающих сил действующих в системе весло-лодка-гребец – очень нетривиальная задача, и получение их точного баланса до сих пор не стало возможным, даже с 11 измеряемыми параметрами для каждого весла. Измерение осевой силы на внешнем рычаге может помочь сложить головоломку, но это очень технически непростая задача. Эксперименты с одновременным тестированием весел могут помочь выяснить их эффективность и КПД на основе соотношения скорость/мощность, что мы планируем выполнить в ближайшее время.

Благодарим компанию Concept2 Inc. и лично Дика Дрессигакера и Алекса Данна за проявленный интерес и поддержку этого исследования.

©2020 Валерий Клешнев

Таблица 1. Средние за проводку величины нормальной силы на вертлюге Fgn, силы на оси FpX, и суммы сил Foar на рукоятке Fhn и лопасти Fbn.

Таблица 2. Средние за проводку величины продвигающих сил системы Fsys и лопасти FbX и их отношение R = Fsys/FbX.