Мощность и кинетическая энергия гребли

Мы продолжаем анализ мощности гребли и ее превращения в кинетическую энергию, используя определения и данные из НБГ 2019/01-02. Основные уравнения движения системы гребец-лодка соотносят силы приложенные к компонентам с их массами и ускорениями. Общая сила, приложенная к лодке F_b есть разность между продвигающей силой F_bp и сопротивлением F_dr:

F_b = F_bp - F_dr =Fp_x – Fs_x - F_dr = m_b a_b (1)

где Fp_x – горизонтальный (Х) компонент силы на оси уключины, Fs_x - Х сила на подножке, m_b a_b - масса и ускорение лодки. В противоположность лодке, которая пассивна в этом случае, гребец – активный компонент системы: он сам прикладывает силы к гребному инвентарю. Поэтому, масса гребца двигается под воздействием сил реакции, которые имеют одинаковую величину и противоположное направления с силами действия: гребец толкает подножку назад и сила реакции F’s_x ускоряет его ЦМ вперед, тянет рукоятку и сила реакции F’h_x двигает его назад. Результирующая сила приложенная к ЦМ гребца F_r также есть разность между продвигающей силой F_rp и сопротивлением F_rr (аэродинамическим), которое очень мало и может быть опущено:

F_r= F_rp – F_rr ~ F’s_x– F’h_x = m_r a_r (2)

где m_r a_r – масса и ускорение гребца. Сила приложенная ко всей системе есть сумма сил гребца и лодки:

F_s = F_b + F_r = (Fp_x – Fs_x - F_dr) + (F’s_x– F’h_x– F_rr) = Fp_x – F’h_x - F_dr = m_b a_b + m_r a_r = m_sa_s (3)

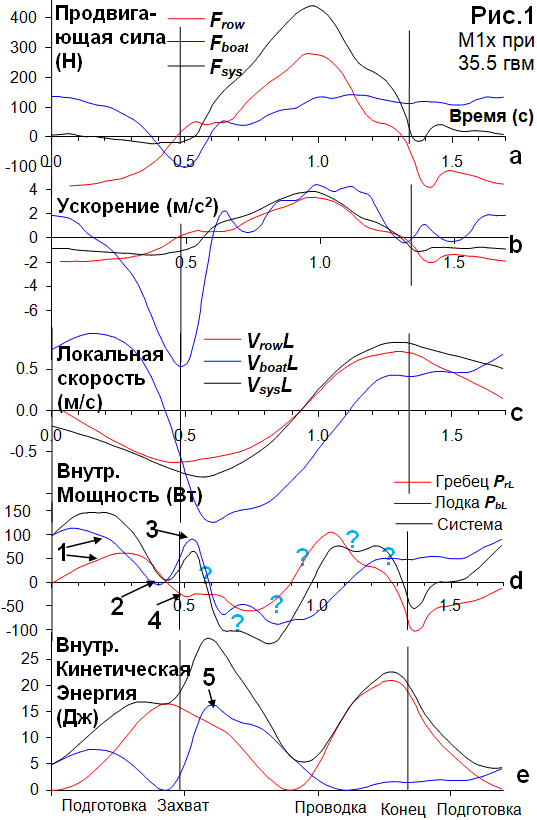
Имея силы F приложенные к ЦМ лодки, гребца и всей системы (Рис.1a) и их массы m, мы можем определить их ускорения a (Рис.1b, здесь следует использовать общую силу на лодке включая силу сопротивления):

a = F / m (4)

Скорости v могут быть получены интегрированием ускорения и добавлением поправки v_off , которая делает среднюю скорость за цикл раной нулю:

v_Li =v_Li_-1 + a _dt + v_off (5)

Скорости v_L (Рис.1с) здесь представлены в локальной инерциальной системе координат, которая движется с постоянной скоростью, равной средней скорости гребли за цикл гребка. В механике, эта система координат называется «координатами центрального момента»: «Кинетическая энергия системы зависит от выбора системы координат: система дающая минимальное значение этой энергии есть координаты центрального момента , т.е. система в которой общий момент равен нулю. Эта минимальная кинетическая энергия дает инвариантную массы системы, как единого целого».

Для получения абсолютных скоростей в глобальных координатах относительно воды v_G, следует добавить среднюю скорость гребли за цикл v_av:

v_G = v_L + v_av (6)

Как мы обсуждали ранее (НБГ 2018/11), здесь возможны два сценария:

· Внутренняя передача мощности между компонентами системы, где должны использоваться скорости в локальных координатах.

· Внешний обмен мощностью со средой, где следует использовать глобальные скорости.

Внутренняя (локальная) мощность определяется, как произведение продвигающих сил (без силы сопротивления) и локальных скоростей ( P_L=F_pv_L, Рис.1d), и кинетическая энергия может быть найдена через массы компонентов ( E_kL=0.5mv_L², Рис.1e).

Обсудим сначала внутреннюю энергию. На подготовке, лопасть весла находится вне воды, поэтому нет продвигающей силы, и лишь одна внешняя сила сопротивления приложена к корпусу лодки, а значит и к системе в целом. Все другие силы – внутренние, поэтому их мощности должны определятся со скоростями в локальных координатах. Опуская малую силу сопротивления гребца, мощность приложенная к его ЦМ P_rL есть:

P_rL = F_r v_rL = (F’s_x– F’h_x) v_rL (7)

Локальная мощность лодки P_bL i:

P_bL = F_bp v_bL = (Fp_x – Fs_x) v _bL (8)

Внутренняя мощность системы определяется, как сумма мощностей лодки и гребца P_sInt и показывает энергию потраченную на внутренние движения в системе:

P_sInt = P_rL + P_bL (9)

Произведение силы и скорости ЦМ системы определяет движение системы, как целого, но это применимо лишь в глобальных координатах, поскольку на систему в целом действуют лишь внешние силы:

P_sG = F_sp v_sG = (Fp_x – F’h_x) v_sG (10)

На подготовке, обе локальные мощности гребца и лодки положительны (1), поскольку их силы и локальные скорости действуют в одном направлении: для гребца, они отрицательны (он тянет себя назад за подножку, и его ЦМ также двигается назад); сила и локальная скорость лодки положительны (ее тянут вперед за подножку и ее скорость выше среднецикловой).

В общем, положительная мощность означает преодолевающее (концентрическое) сокращение мышц: сила и скорость действуют в одном направлении (обе положительны или обе отрицательны, в зависимости от системы координат) и мышцы производят энергию. Отрицательная мощность означает уступающее (эксцентрическое) сокращение мышц: сила и скорость действуют в противоположных направлениях, и мышцы поглощают механическую энергию произведенную где-то еще.

Перед захватом, мощность лодки становится близка к нулю на короткое время (2), поскольку сила и скорость меняют направление. Затем, мощность лодки снова возрастает (3), так как и сила, и локальная скорость становятся отрицательными одновременно. Внутренняя мощность гребца становится отрицательной перед захватом (4), поскольку сила становится положительной, но локальная скорость остается отрицательной и лишь немного начинает увеличиваться: масса гребца намного больше и не может изменить направление движения также быстро, как лодка. Здесь, мы встречаем типичный пример столкновения двух масс.

Из механики, существуют два противоположных типа столкновений: упругие, как бильярдные шары, которые отскакивают друг от друга в противоположных направлениях после столкновения почти с такой же скоростью, как и до него, и неупругие, как два куска глины, которые слипаются и двигаются, как одно целое после столкновения. В обоих случаях, общий момент движения системы не изменяется, как это диктуется законом сохранения момента. Однако, внутренняя кинетическая энергия системы (сумма энергий ее компонентов) очень различна:

· При абсолютно упругих столкновениях, объекты обмениваются своей кинетической энергией, поэтому внутренняя энергия системы остается постоянной (энергия – скалярная величина, а не вектор) .

· При неупругих столкновениях, кинетическая энергия тратится на деформацию объектов и рассеивается в виде тепла, поэтому внутренняя энергия системы становится равна нулю: внутренние движения в системы исчезают после столкновения.

Конечно, в чистой механике не существует абсолютно упругих столкновений, поскольку часть энергии всегда расходуется на деформацию объектов, но в живом мире, энергия может быть добавлена сокращением мышц. Биомеханические исследования с элитными бегунами-спринтерами показали, что до 90% энергии отталкивания обеспечивается упругими свойствами сухожилий, и лишь 10% добавляется мышцами. Конечно, движения в гребле намного медленнее и сложнее организованы, и такой КПД выглядит проблематично. Однако, чем более упругое столкновение происходит между гребцом и лодкой в захвате, тем больше кинетической энергии сохраняется, ее можно снова использовать на проводке, что увеличивает КПД гребли. Это означает, что эффективный захват должен выглядеть, как «отскакивающий мяч» . Это прекрасно подтверждает наши предыдущие концепции «захвата через подножку», «эффекта трамплина» и «принципа молотка и гвоздя», и добавляет еще один аргумент против устаревших идей «не останавливать лодку», «поддерживать ее скорость в захвате» и т.п. Рис.1е показывает, что кинетическая энергия лодки после захвата (5) становится выше, чем на подготовке, что означает эффективную технику данного гребца.

Если столкновение масс в захвате неупругое, гребец должен поглотить кинетическую энергию движения на подготовке, что все равно утомляет его мышцы, а затем произвести энергию снова мышцами для начала проводки, поэтому КПД снижается. Наихудшее, что может сделать гребец – это замедлить движение банки во второй половине подготовки и «прилипнуть к подножке» в захвате.

Во время проводки, картина намного усложняется, поскольку добавляется внешняя мощность от весла, которая смешивается с внутренней, поэтому мы поставили знаки вопроса в Рис.1d. Внешние мощности компонентов системы можно определить по уравнениям, аналогичным 7-10, где глобальные скорости заменяются локальными. Однако, на подготовке, глобальные мощности лодки и гребца не валидны, поскольку на них не действуют внешние силы, поэтому они зачеркнуты. Глобальные мощности системы можно определить двумя способами: как сумму мощностей гребца и лодки, и как произведение продвигающего усилия и скорости:

P_sG = F_sP v_sG = (Fp_x – F’h_x ) v_sG (11)

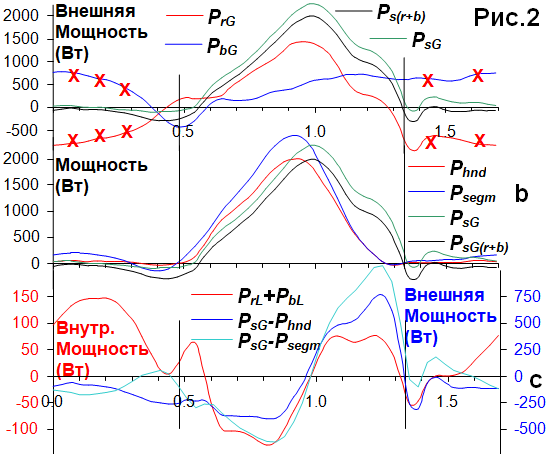
Рис.2b сравнивает обе мощности системы выше с традиционной мощностью на рукоятке и суммой мощностей сегментов тела (НБГ 2004/06). Средняя мощность системы P_sG₍_r₊_b₎ была близка к таковой на рукоятке P_hnd (±3% при 17-41 гвм), P_sG были похожи на P_segm (±5%), а размах вариации кинетической энергии системы был близок к измеренной работе за гребок (±2%).

Рис.2с сравнивает внутреннюю мощность системы из Рис.1d (по левой шкале) с разностями между глобальной кинетической и мощностью гребца (по правой шкале). Кривые выглядят достаточно похоже, что подсказывает гипотезу об объяснении вторых влиянием первых, но проблема в том, что глобальные разности оказались в 4-5 раз больше, чем локальные мощности.

Мы продолжим анализ в следующем бюллетене и будем благодарны за все комментарии и идеи.

Теги: Мощность и кинетическая энергия гребли