HDF в течение гребка

В этой статье мы продолжаем предыдущее исследование Коэффициента Сопротивления Рукоятки HDF (НБГ 2020/01). На самом деле, HDF не безразмерен, также, как и DF лодки, лопасти или эргометра, и имеет размерность кг/м:

DF(or HDF) = P/v3 = (kg m2/s3)/(m3/s3) = kg/m        (1)

Это следствие общего уравнения коэффициента сопротивления Cd тела движущегося в жидкости или газе:

Cd = 2 Fd / (ρ A v2)                                                     (2)

где Fd – сила сопротивления, ρ – плотность жидкости или газа, A – относительная площадь сечения тела, v – скорость движения. Cd действительно безразмерен и зависит лишь от формы тела и характера потока (ламинарный или турбулентный). Объединяя уравнения выше,

DF = Fd/v2 = Cd ρ A / 2 = (kg/m3) m2 = kg/m           (3)

Поэтому, DF - комбинация формы (Cd) и размера (A) движущегося тела с плотностью среды (ρ), что можно интерпретировать, как массу жидкости или газа, перемещенную за каждый метр движения тела. HDF и DF имеют одинаковую размерность и значение: они оба индикаторы соотношения силы сопротивления к скорости.

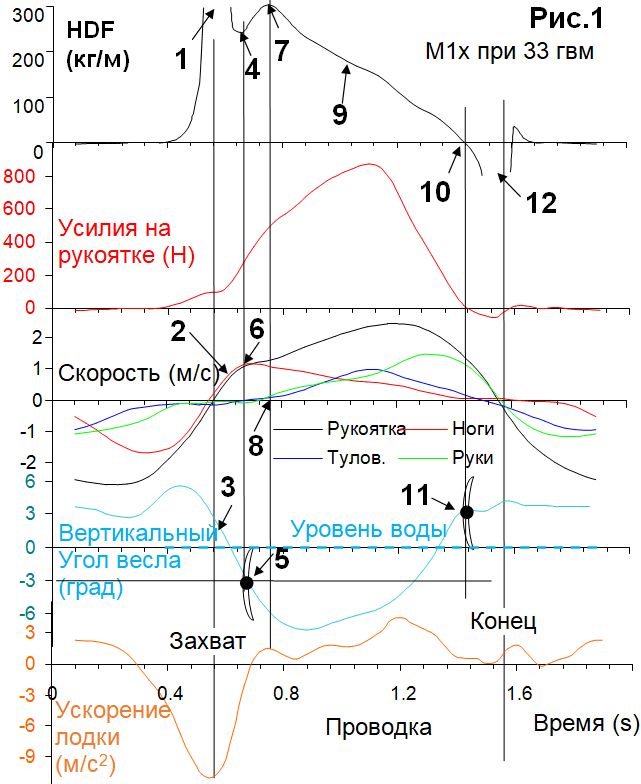
Уравнение 3 позволяет определить мгновенные значения HDF на проводке по измеренным скорости и усилиям на рукоятке (Рис.1):

HDF не определен (равен бесконечности ∞) в захвате (1), когда скорость рукоятки пересекает ноль. Затем HDF снижается, при резком росте скорости рукоятки (2) и входе лопасти в воду (3). Примерно после 8-10% времени проводки, HDF имеет впадину (4), которая совпадает с полным входом лопасти в воду (5), которая затем продолжает погружение. Кривая скорости рукоятки здесь изгибается, ее рост замедляется, и HDF возрастает, достигая своего пика (7) через 18-20% времени проводки. Пик HDF достигается сразу после пика скорости ног, когда начинают работать туловище и руки (8) и ускорение лодки достигает первого пика. Этот момент можно назвать «запирание лопасти» (выражение Фолькера Нольте). После пика, HDF постоянно снижается (9), поскольку динамическое передаточное отношение весла становится «легче». HDF становится отрицательным перед концом проводки (10), когда сила на рукоятке становится отрицательной (из-за инерции весла) и лопасть уже полностью вышла из воды (11). В конце проводки (12), HDF снова не определен (=-∞), когда скорость рукоятки пересекает ноль.

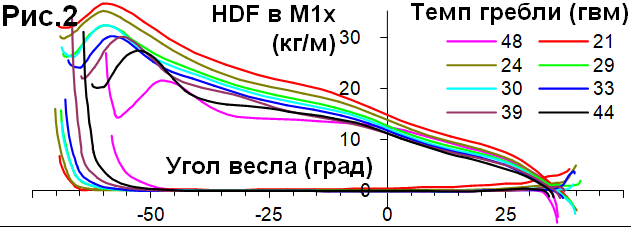
Характер кривой HDF довольно постоянен при различных темпах и стилях гребли (Рис.2):

У этого одиночника, угол захвата становится короче при повышении темпа, поэтому величина HDF снижается, что было отмечено ранее (НБГ 2020/01). Однако, впадина наблюдается через те же 8-10% времени проводки и 3-4% ее длины, относительное время и место достижения пика сохраняется и величины HDF во второй половине гребка остаются примерно постоянны.

При расчетах средних величин HDF за цикл гребка, использование средних усилий Fav в ур.3 даст более высокие значения в сравнении с мощностью P в ур.1, поскольку Fav определяется лишь за фазу проводки, а мощность P распределяется на все время цикла. Поэтому, средний HDF за цикл гребка нужно умножить на значение ритма (отношение времени проводки ко времени всего цикла), чтобы получить величины, опубликованные ранее в НБГ 2020/01.

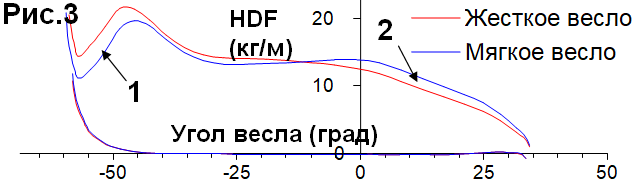
Интересно, как жесткость весла влияет на характер HDF и ощущения гребца (Рис.3):

Менее жесткое весло больше изгибается после захвата, когда усилия возрастают, что делает скорость рукоятки несколько выше, HDF ниже (1) и ощущения гребца «легче». Когда усилия снижаются во второй половине проводки, мягкое весло «отпружинивает» больше и позже, что замедляет скорость рукоятки, HDF увеличивается и гребец чувствует больший упор. Это значит, что менее жесткое весло делает HDF и ощущения гребца более постоянными во время проводки.

Благодарности. Благодарю проф. Фолькера Нольте за продуктивную дискуссию по данной теме.

©2020 Валерий Клешнев