Коэффициент сопротивления лопасти
В фазе проводки, лопасть «проскальзывает» через воду и создает силу сопротивления, которая и является продвигающей силой для всей системы гребец-лодка. Чем меньше сплывание лопасти, тем выше КПД лопасти. Однако, последний зависит от скорости лодки (НБГ 2012/06), которая отличается в различных классах лодок, погодных условиях и в фазах цикла гребка, что затрудняет оценку КПД. Поэтому, мы предложили использовать для оценки работы весла метод аналогичный коэффициенту сопротивления лодки DF:
DF = Fdr / v2
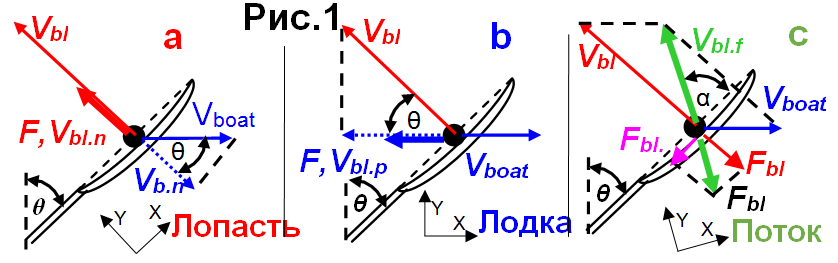
Где Fdr - сила сопротивления, v - скорость объекта, движущегося в жидкости. В случае движения лодки, определить просто, поскольку скорость лодки линейна и сила сопротивления работает по той же линии. Однако, траектория лопасти криволинейна (НБГ 2007/12), поэтому, неясно какую силу и скорость использовать в уравнении 1. Здесь возможны, как минимум, три варианта, которые зависят от выбора системы координат (Рис.1):

1. В координатах лопасти (которые вращаются вместе с ней на проводке), Коэффициент Сопротивления Лопасти Нормальный BDFn определяется через скорость лопасти Vbl.n относительно воды в перпендикулярном направлении к оси весла:
Vbl.n = Vbl – Vboat * cos θ (2)
где Vbl – нормальная скорость лопасти относительно лодки (вычисленная из измеренной угловой скорости и реального внешнего рычага), Vboat – измеренная скорость лодки, θ – измеренный угол весла.
BDFn = Fbl / Vbl.n2 (3)
где Fbl – нормальное усилие на лопасти (по измеренной силе на рукоятке и передаточного отношения весла).
2. В координатах лодки, Продвигающий BDFp определяется через скорость лопасти Vbl.p относительно воды в направлении, параллельном оси лодки – в продвигающем направлении, поэтому:
Vbl.p = Vbl * cos θ – Vboat (4)
BDFp = Fbl cos θ / Vbl.p2 (5)
3. Если рассматривать лопасть, как объект движущейся через воду, то сопротивление относительно потока BDFf определяется величинами векторов скорости воды относительно лопасти Vbl.f и силы сопротивления Fbl.f в направлении, противоположном вектору скорости. В этом случае, система координат привязана к вектору потока воды в каждый момент времени, величину которого Vbl.f можно рассчитать, как:
Vbl.f = (Vbl2+Vboat2-2*Vbl*Vboat*cos(θ))0.5 (6)
Направление вектора потока определяется углом весла θ и углом атаки лопасти α, который вычисляется, как:
α = asin((Vbl.f2 + Vbl2 - Vboat2) / (2 Vbl.f Vbl)) (7)
Величина силы сопротивления Fbl.f – есть векторная сумма нормальной Fbl и осевой Fbl.a сил, но последняя не измерялась в данном случае, что является ограничением точности метода. Hofmijster et al. (1) нашел эту осевую силу Fbl.a в диапазоне 10-13 Н, что составляет лишь 6-8% от нормальной силы Fbl, поэтому сила в направлении потока Fbl.f и BDFf можно рассчитывать лишь на основе Fbl без значительной погрешности:
BDFf =Fbl.f / Vbl.f2 = (Fbl * sin α) / Vbl.f2 (8)
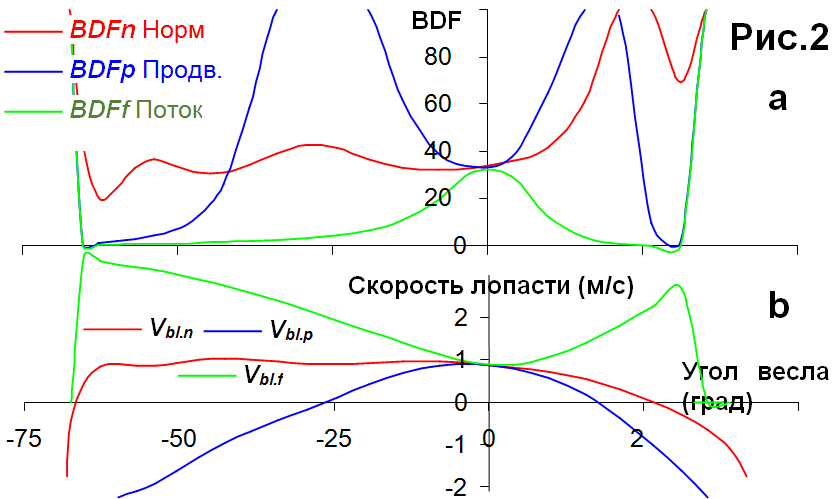
Рис.2,а показывает все три коэффициента сопротивления при гребле в одиночке на темпе 34,5 гвм (сумма двух весел) совместно с соответствующими скоростями лопасти. Как это и должно быть, все три коэффициента почти равны друг другу на уровне около 350 при нулевом угле весла, когда скорость лопасти на 100% продвигающая (направлена параллельно лодке) и скорость потока воды перпендикулярна лопасти, поэтому и равна ее скорости .

При других углах весла, коэффициенты ведут себя очень различно:
· BDFn наиболее постоянен от захвата до угла весла 0о, а затем возрастает до бесконечности, когда кривая скорости лопасти Vbl.n пересекает нуль. После этого, он снова снижается до нуля, поскольку сила на лопасти снижается, а скорость снова возрастает, но в обратном направлении: лопасть ускоряется вперед по ходу лодки.
· BDFp достигает бесконечности дважды на проводке, при -25 и 20о, когда Vbl.p пересекает нулевую линию от негативных значений (к носу лодки) – к позитивным (к корме), и снова к негативным. После захвата и перед концом гребка, этот коэффициент близок к нулю, поскольку сила на лопасти мала, а центр лопасти быстро движется вперед вместе с лодкой.
· BDFf имеет низкие величины в начале и в конце проводки, поскольку скорость потока воды велика при острых углах атаки, а сила в этом направлении низка. Этот коэффициент никогда не достигает бесконечности и его кривая имеет плавную форму колокола.
Интересно сравнить DF лопасти с DF лодки, который был 2,95 в данном случае, так что DF лопасти был примерно в 120 раз выше, и это является единственной причиной, которая позволяет системе гребец-лодка двигаться через воду.
Литература
1. Hofmijster M., Koning J., Van Soest A. 2010 Estimation of the energy loss at the blades in rowing: Common assumptions revisited. Journal of Sports Sciences, p. 28(10): 1093–1102
©2018 Валерий Клешнев